
高中选课走班排课可能存在的四大误区
随着中高考改革的实施和扩展,关于走班教学的选课排课策略成为教育热点话题,目前,实行走班教学的学校大致可分为三类:小走班、中走班、大走班。
- 小走班 是在6选3(或7选3)的学科范围内限制性走班,即采用套餐制,把原来的文理两种组合改为4—8种组合,牺牲掉一部分学生的选科意愿;
- 中走班 是在6选3(或7选3)范围内实现较大程度走班,但很多学校采用“定二选一”“双向聚焦”“2(等级与合格合并)+1(等级考)”等诸多形式减少排课组合数量,减少排课难度;
- 大走班 是全体学生的全学科走班,语数外分层、选考科目分类、体艺及校本课程分项,这是走班教学的成熟形态。
很多沪浙校长在介绍经验时,往往津津乐道于如何降低排课难度,包括给学生和家长反复做工作使其放弃自己的选择组合,最终减少组合数量,甚至有学校经过与学生和家长的“有效沟通”,让所有学生又回到文理分科的状态(浙江某学校校长到全国介绍此经验)。校长为了实现自己的管理目的,还会从学生需要集体观念、同伴交往和归属感等诸多方面论证学校限制学生选择的“合理性”,其实,这种做法违背中高考改革的初衷、没有尊重学生的学习自主权和课程选择权,校长心知肚明。
外地校长参观学习时之所以对排课策略的趋之若鹜、如饥似渴,很大程度上源于上海、浙江校长总结的种种“经验”形成的排课误区。
误区之一:走班教学对学校的资源要求特别高,普通的高中根本无法实现大走班。众所周知,学校的任何教学组织形式,都需要相应的教师、课程、教室资源做支撑。是不是走班教学后,对各种资源的需求就会飙升,而使学校无法满足呢?显然不是这样。走班教学,说到底是组织教学过程对现有学生时间、空间的重新设置,是对各种资源的重组和优化配置,理论上现有资源足够使用。事实上,很多学校在没有增加任何资源的情况下实现了大走班教学,保证满足了学生的全部选课意愿。
为什么会出现这种情况呢?我们可以就广东越秀外国语学校的学生选课数据做具体分析。广州越秀外国语学校为了提前适应高考改革背景下的走班教学新形式,2016年开始排走班课表,通过对学生选课数据的统计分析(如下图),在不增加任何资源的情况下利用计算机软件顺利排出走班课表。
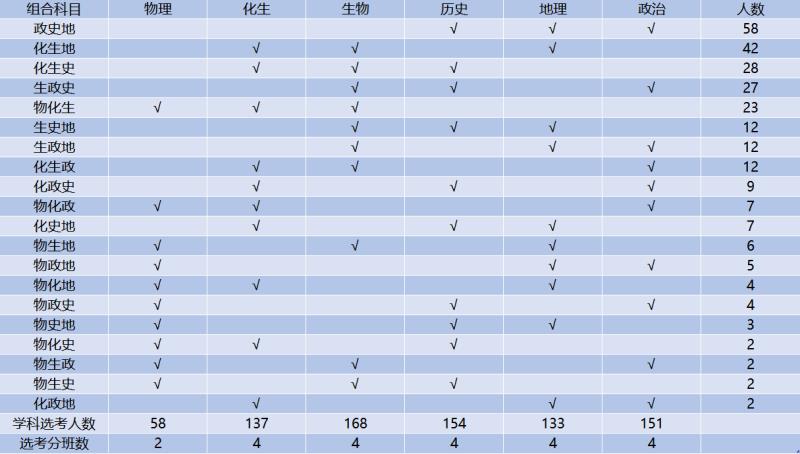
在排课表时,计算机和人的思维完全不同:受计算能力的限制,人在排课时考虑的是组合(权且称之为“组合排课思维”),在上图中就看到,267名高二学生在全部20中组合中(纵向第8列数据),有12种组合选择人数不足10人,这样看来,资源就远远不够;而计算机软件不考虑组合,只考虑每个学科的选考人数(横向第22行数据),排课只依据每个学科的选考人数(可称为“学科排课思维”),通过计算各种排课条件中学生的互斥关系,再加上学校的各项排课规则,通过上百亿量级的计算,选课结果统计、分班、排课、生成课表一步到位。更重要的是,计算机软件的“学科排课思维”是对学校各种资源的最优化配置,对资源几乎不提出更多要求(特别极端的选课数据除外),便于学校合理均衡使用现有资源,实现满足全部学生意愿的走班教学。
误区之二:学校规模小,不能采用全走班。如上所分析,走班教学是对现有资源的重组和优化配置,并不需要增加更多教师、教室、课程资源。相反,规模小的学校,更加依赖于计算机软件技术,通过排课软件排出合理的课表。
误区之三:沪浙很多学校都没有采用软件,可以通过限制选择手工排出课表。2017年上海、浙江高考报名结束后,考试招生部门做了统计,传统文理科的学生人数不到四分之一,说明,尽管有很多学校捆住了孩子选择的双手,还是有相当数量的学生打破文理科界限,选择了自己喜欢且擅长的学科作为选考(上海称“等级考”)科目。所以,把充分的选择权还给学生,是大势所趋,无法阻挡。这里需要搞清楚一个逻辑关系:不是因为限制选择,才不用软件排课,而是因为没有高级算法支持的先进软件支持,不得不限制学生的选择。
误区之四:学生的选择权利越充分,越不利于集中优势力量抓高考。有这种意识的校长为数不少,充分说明对新高考的理解还不够透彻。新的高考采用不同学科等级赋分的方式,不同的学科组合有不同的录取分数线,人为限制学生选择,在多种组合的高考选拔中出现孔项,不利于学校高考成绩的整体提升,加之,有很多原本擅长某些学科组合的学生被迫放弃,无论对于学习积极性和是学习成绩都会产生巨大的负面影响。所以,不要听很多学校限制选择做出的很多辩解,而要看到限制选择在很大程度上是排课技术不支持的一种无奈的选择。
面对市场上良莠不齐的各种排课软件,校长们经常眼花缭乱,不知所措。其实,对排课软件的判断需要抓住实质,只需了解“是否支持先选后排,满足学生的全部选科意愿,并支持现场排课?”这是所有排课软件的“试金石”,能够充分实现学校各种资源的优化配置、排出科学合理便于操作和评价的课表,一试便知。
目前,在第二批第三批进入高考的北京、天津、山东、广东、四川等省市,已经有多所名校正在享受先进排课软件技术带来的便捷高效。例如:北京三十五中、潞河中学、育英中学、中国矿业大学附中、北京科技大学附中、北京石油学院附中、北京八一学校国际部、天津第二南开学校、山东青岛高级实验中学、山东高青一中、广州越秀外国语学校,北大附属德爱实验学校、成都石室联合中学等。
荀子曰:“君子性非异也,善假(借)于物也”。面对中高考改革的大趋势,有远见卓识的校长会坚定“以学生发展为本”的信念,借助先进技术的力量,破解走班教学的排课难题,并全面提升教育教学质量。
作者:刘文江(现任钱学森教育思想研究会副会长,中国下一代教育基金会智慧教育基金秘书长)
